1. Minimax Algorithm
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case (maximum loss) scenario.
틱-택-토, 체스, 오목과 같은 게임의 인공지능은 어떻게 만들어질까?
저런 게임들은 멀리 보는것이 중요하다. 상대방을 파악하고 예상해서 장기적으로 유리하게 이끌어 가야 이기게 된다.
컴퓨터는 게임의 판도를 읽을 줄 모르기 때문에, 게임판의 상태를 점수로 변환시키는 과정이 필요하다. 예를 들면 체스에서 폰은 1점, ..., 퀸은 9점 하는 것과 같이 이 과정을 '평가한다'고 하자. 평가하는 규칙을 정한다면 게임판의 모든 상태를 점수로 바꿀 수 있다.
여기에 "AI가 유리하면 큰 점수, 유저가 유리하면 작은 점수"가 되도록 규칙을 잘 정해주면 된다. (사실 어떻게 보면 이 과정이 가장 어렵다.)
컴퓨터가 이길 수 있는 방법은, 지금 게임판의 상태에서 변경 가능한 모든 경우를 평가해서, 가장 높은 점수의 길로 가는 것이다. 그런데, 이런 상황이라면?
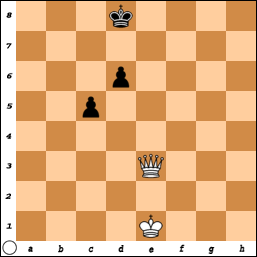
이때, 컴퓨터인 흰색 퀸이, 다음 차례에 가장 유리해지도록 C5로 가서 폰을 먹는다면, 곧 D6의 폰에게 퀸을 잃게 될 것이다. 이처럼, 평가해야할 게임판은 바로 당장의 게임판이 아닌, 몇수 후의 게임판을 평가해서, 가장 높은 점수의 평가판을 향해 다음 수를 두어야 한다.
하지만 그럴때 상대편은 항상 우리에게 최악인 수를 골라서 간다. 왜냐면 그래야 자기들이 이기기 때문이니까. 그래서 우리는 상대편이 던저주는 최악의 수 중에서, 가장 최선의 수를 골라야 한다.
그래서 이용되는 알고리즘이 Minimax 알고리즘이다.

위의 그림을 분석해보자. 현재 상태은 가장 위에 있는 0번째 상황이고, 이 인공지능은 4수를 내다볼 수 있다. 4수째의 상태 중에서 최고의 상태은 가장 왼쪽의 점수가 10인 상태로 가는 것이다. 하지만 그렇다고 현재 선택에서 왼쪽길을 선택한다면, 상대방은 자신에게 가장 유리한 점수가 -10인 상태로 갈 것이다. 결국 본전도 못찾은것. 결국 가장 나은 길은 오른쪽 길이다.
이렇게 분석하는 Minimax 알고리즘을 간단한 애니메이션으로 보자.
위키피디아의 의사 코드도 살펴보자.
function minimax(node, depth, maximizingPlayer)
if depth = 0 or node is a terminal node
return the heuristic value of node
if maximizingPlayer
bestValue := -∞
for each child of node
val := minimax(child, depth - 1, FALSE))
bestValue := max(bestValue, val);
return bestValue
else
bestValue := +∞
for each child of node
val := minimax(child, depth - 1, TRUE))
bestValue := min(bestValue, val);
return bestValue
(* Initial call for maximizing player *)
minimax(origin, depth, TRUE)
그런데, 실제 게임은 가짓수가 어마어마하게 많다. 한가지 상태에서 10가지 경우가 나온다면, 3수 앞을 내다보는 인공지능은 1000가지 상태를, 6수 앞을 내다보는 인공지능은 1000000가지 상태를 평가해야 한다. 그래서 저 연산 중 불필요한 연산을 가지치듯이 버리는 알고리즘인 알파-베타 가지치기(Alpha-beta pruning)이 등장한다.
2. 알파-베타 가지치기
기본 Minimax 알고리즘은 모든 노드를 방문해서 평가해야 했지만, 실제로는 그렇지 않아도 되는 경우가 존재한다.
- 자신이 그 경우를 택하면 자신이 불리해지는 것이 확정된 경우
- 어떠한 경우가 자신에게 유리한 것이 확정되어 상대가 그것을 택하지 않을 확률이 높은 경우
두 경우는 애써 모든 자식노드를 검사해봐야 선택하지 않을 확률이 매우 높다. 그래서 저러한 경우가 확정되면 그 노드의 자식노드에 대한 평가를 당장 중지하여야만 불필요한 연산을 줄일 수 있다.
약간 길지만 자세한 동영상 설명을 보자.
그리고 위키피디아의 의사코드를 음미해보자.
function alphabeta(node, depth, α, β, maximizingPlayer)
if depth = 0 or node is a terminal node
return the heuristic value of node
if maximizingPlayer
for each child of node
α := max(α, alphabeta(child, depth - 1, α, β, FALSE))
if β ≤ α
break (* β cut-off *)
return α
else
for each child of node
β := min(β, alphabeta(child, depth - 1, α, β, TRUE))
if β ≤ α
break (* α cut-off *)
return β
(* Initial call *)
alphabeta(origin, depth, -∞, +∞, TRUE)
위의 동영상을 보면, Alpha 는 이전(상위) 상태들 중에서 AI에게 가장 유리한 상태의 점수, Beta 는 이전(상위) 상태들 중에서 상대방에게 가장 유리한 상태의 점수이다.
Alpha cut-off 는 자신이 상대방보다 불리하여, 자신이 그 경우를 선택하지 않을 때 불필요한 연산을 잘라내는 것이고, Beta cut-off 는 자신이 상대방보다 유리하여, 상대방이 그 경우를 선택하지 않을 확률이 높을 때 불필요한 연산을 잘라내는 것이다. 둘의 차이점을 잘 알아두자.
3. 마무리
Alpha-beta pruning 외에도 Negascout 이나 MTD-f 와 같은 최적화 알고리즘이 있다고 한다. 이건 나중에 알아보자.
AS3으로 직접 Reversi의 인공지능을 구현해보았다. Depth가 커질수록 강한 인공지능이 되지만 랙은 기하급수적으로 커진다. 5 정도 되면 느려지기 시작하고 6 이상은 정상적인 플레이가 힘들정도..
'PYTHON' 카테고리의 다른 글
| Python 2.7 installing opencv via pip (virtual environment) (0) | 2021.05.10 |
|---|---|
| 파이썬 프로그래밍 입문서 (0) | 2020.12.11 |
| [Python] Numpy 배열(생성, 색인, 연산 ..) (0) | 2020.12.09 |
| [python] numpy array 특징과 사용법 (0) | 2020.12.09 |
| 파이썬 numpy - array 생성 함수 ones, zeros,empty (0) | 2020.12.09 |