Single-length Key KCV
The single-length key check value is a one-way cryptographic function of a key, used to verify that the key has been entered correctly.
The KCV is calculated by taking an input of constant D (64 Zero bits) and encrypting it with key K (64 bit). The 64 bit output is truncated to the most significant 24 bits which is reported as the keys KCV (Single-length Key Check Value KCV(K).).
Figure 1: Single-length Key Check Value KCV(K).

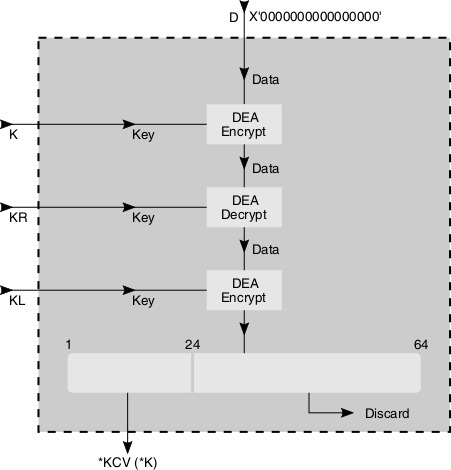
Double-length Key KCV
The double-length key check value is a one-way cryptographic function of a key, used to verify that the key has been correctly entered.
The KCV is calculated by taking an input of constant D (64 Zero bits) and key *K (128 bit string made up of two 64 bit values KL and KR ). Data value D is encrypted with KL as the key. The result is decrypted with KR as the key. The result is then encrypted with KL as the key. The 64 bit output is truncated to the most significant 24 bits which is reported as the double-length keys *KCV (Double-length Key Check Value *KCV(*K)).
Figure 2: Double-length Key Check Value *KCV(*K)
'Cryptography' 카테고리의 다른 글
| Configuring the HSM to Operate in FIPS Mode (0) | 2024.04.05 |
|---|---|
| HOTP and TOTP (31) | 2024.03.21 |
| The group Zp* (31) | 2024.03.11 |
| Padding oracles and the decline of CBC-mode cipher suites (117) | 2024.03.08 |
| CBC-bit Flipping (56) | 2024.03.08 |