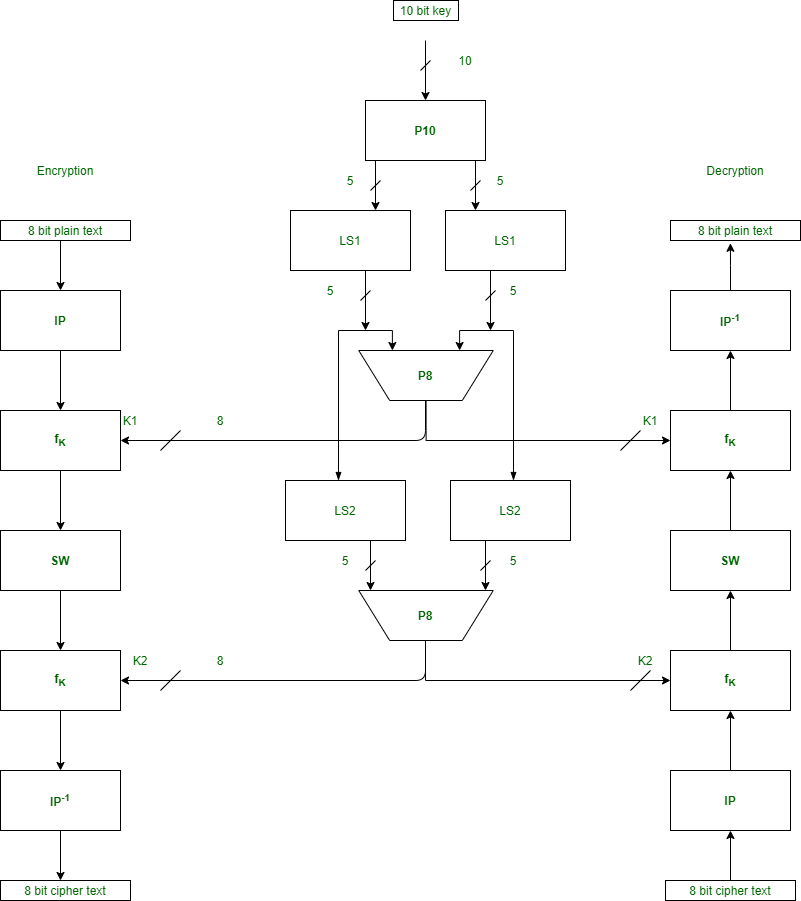
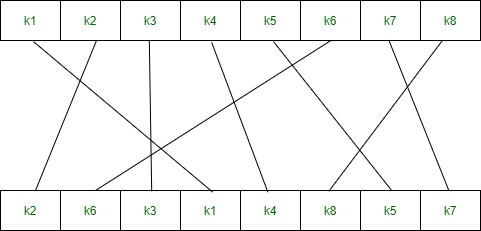
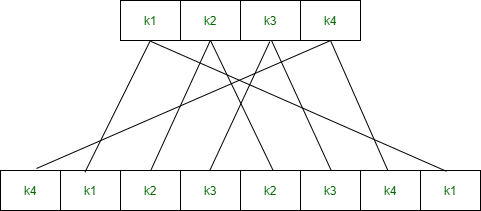
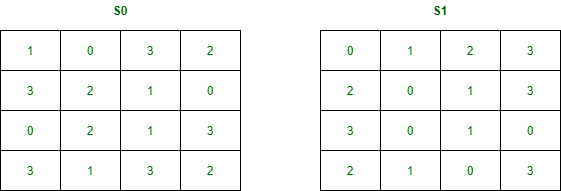
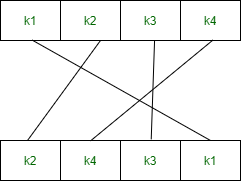
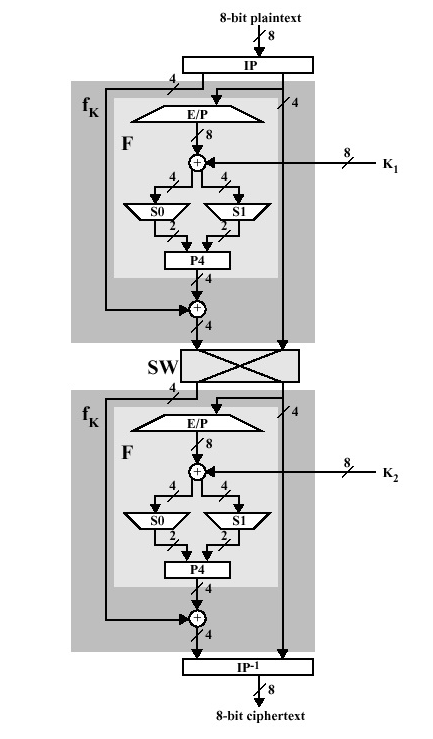
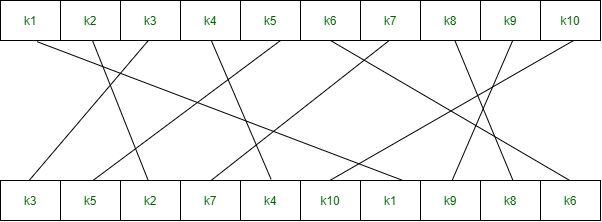
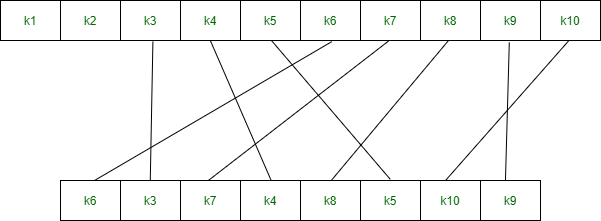
Block ciphers are built in the Feistel cipher structure. Block cipher has a specific number of rounds and keys for generating ciphertext.Block cipher is a type of encryption algorithm that processes fixed-size blocks of data, usually 64 or 128 bits, to produce ciphertext. The design of a block cipher involves several important principles to ensure the security and efficiency of the algorithm. Some of these principles are:
- Number of Rounds – The number of Rounds is regularly considered in design criteria, it just reflects the number of rounds to be suitable for an algorithm to make it more complex, in DES we have 16 rounds ensuring it to be more secure while in AES we have 10 rounds which makes it more secure.
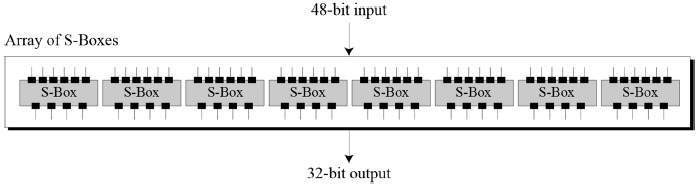
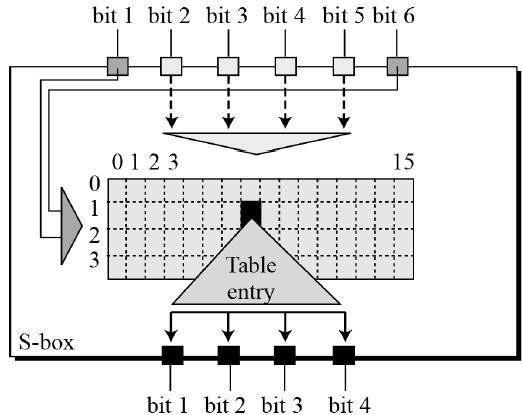
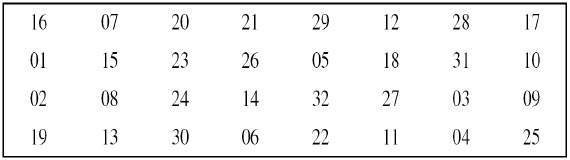
- Design of function F – The core part of the Feistel Block cipher structure is the Round Function. The complexity of cryptanalysis can be derived from the Round function i.e. the increasing level of complexity for the round function would be greatly contributing to an increase in complexity. To increase the complexity of the round function, the avalanche effect is also included in the round function, as the change of a single bit in plain text would produce a mischievous output due to the presence of avalanche effect.
- Confusion and Diffusion: The cipher should provide confusion and diffusion to make it difficult for an attacker to determine the relationship between the plaintext and ciphertext. Confusion means that the ciphertext should be a complex function of the key and plaintext, making it difficult to guess the key. Diffusion means that a small change in the plaintext should cause a significant change in the ciphertext, which makes it difficult to analyze the encryption pattern.
- Key Size: The key size should be large enough to prevent brute-force attacks. A larger key size means that there are more possible keys, making it harder for an attacker to guess the correct one. A key size of 128 bits is considered to be secure for most applications.
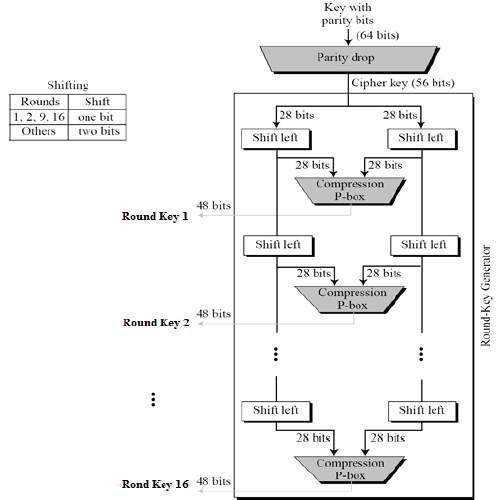
- Key Schedule: The key schedule should be designed carefully to ensure that the keys used for encryption are independent and unpredictable. The key schedule should also resist attacks that exploit weak keys or key-dependent properties of the cipher.
- Block Size: The block size should be large enough to prevent attacks that exploit statistical patterns in the plaintext. A block size of 128 bits is generally considered to be secure for most applications.
- Non-linearity: The S-box used in the cipher should be non-linear to provide confusion. A linear S-box is vulnerable to attacks that exploit the linear properties of the cipher.
- Avalanche Effect: The cipher should exhibit the avalanche effect, which means that a small change in the plaintext or key should cause a significant change in the ciphertext. This ensures that any change in the input results in a complete change in the output.
- Security Analysis: The cipher should be analyzed for its security against various attacks such as differential cryptanalysis, linear cryptanalysis, and brute-force attacks. The cipher should also be tested for its resistance to implementation attacks, such as side-channel attacks.
Overall, a good block cipher design should be resistant to various attacks, efficient, and easy to implement.
'Cryptography' 카테고리의 다른 글
| Meet-in-the-middle attack (0) | 2024.02.29 |
|---|---|
| Block Cipher modes of Operation (31) | 2024.02.29 |
| DES (Data Encryption Standard) (0) | 2024.02.28 |
| Simplified Data Encryption Standard | Set 2 (0) | 2024.02.28 |
| Simplified Data Encryption Standard Key Generation (63) | 2024.02.28 |