Prerequisite –
Simplified Data Encryption Standard is a simple version of Data Encryption Standard having a 10-bit key and 8-bit plain text. It is much smaller than the DES algorithm as it takes only 8-bit plain text whereas DES takes 64-bit plain text. It was developed for educational purpose so that understanding DES can become easy. It is a block cipher algorithm and uses a symmetric key for its algorithm i.e. they use the same key for both encryption and decryption. It has 2 rounds for encryption which use two different keys.
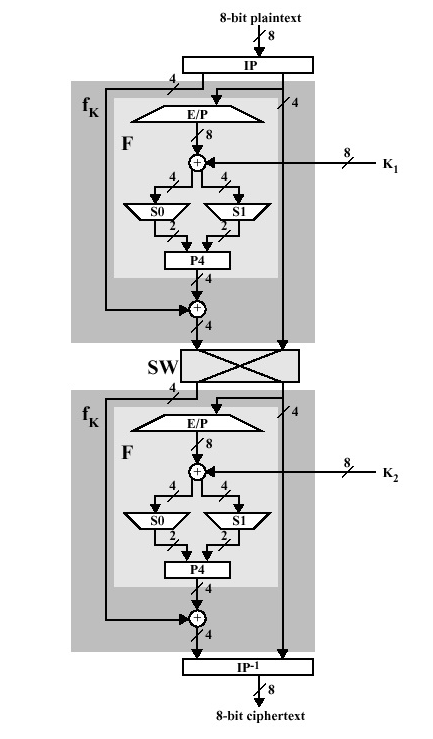
First, we need to generate 2 keys before encryption. After generating keys we pass them to each individual round for s-des encryption. The below diagram shows the steps involved in the s-des algorithm.
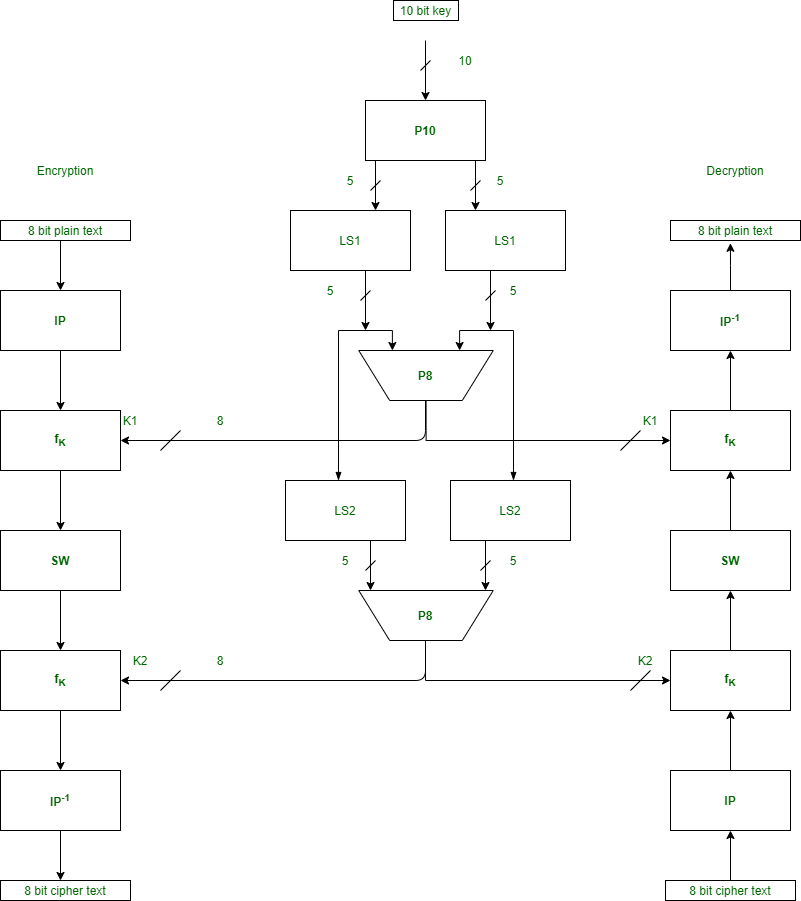
Components :
S-DES encryption involves four functions –
1. Initial permutation(IP) –
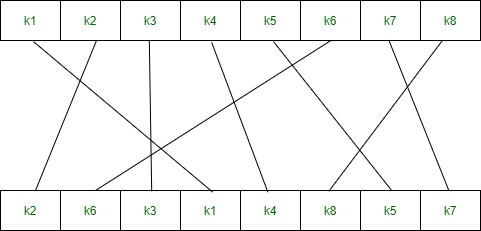
2. Complex function (fk) –
It is the combination of permutation and substitution functions. The below image represents a round of encryption and decryption. This round is repeated twice in each encryption and decryption.

Components in fk are –
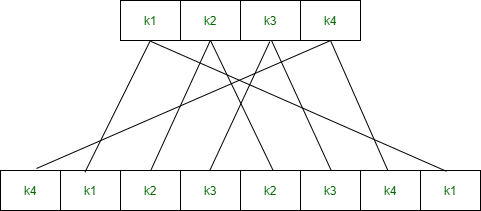
a. Expanded Permutation (EP) –
It takes a 4-bit input and converts it into an 8-bit output.
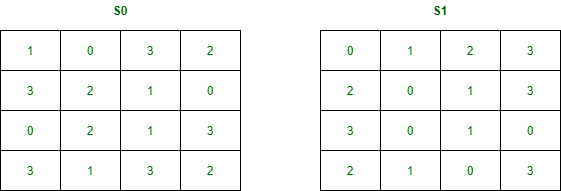
b. S-boxes (S0 and S1) –
It is a basic component of a symmetric key algorithm that performs substitution.
c. Permutation P4 –
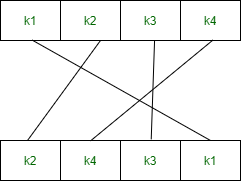
3. Switch (SW) –

4. Inverse of Initial Permutation (IP-1) –

First, we need to generate 2 keys before encryption.
Consider, the entered 10-bit key is - 1 0 1 0 0 0 0 0 1 0
Therefore,
Key-1 is - 1 0 1 0 0 1 0 0
Key-2 is - 0 1 0 0 0 0 1 1
Encryption –
Entered 8-bit plaintext is - 1 0 0 1 0 1 1 1
Step-1:
We perform initial permutation on our 8-bit plain text using the IP table. The initial permutation is defined as –
IP(k1, k2, k3, k4, k5, k6, k7, k8) = (k2, k6, k3, k1, k4, k8, k5, k7)
After ip = 0 1 0 1 1 1 0 1
Step-2:
After the initial permutation, we get an 8-bit block of text which we divide into 2 halves of 4 bit each.
l = 0 1 0 1 and r = 1 1 0 1
On the right half, we perform expanded permutation using EP table which converts 4 bits into 8 bits. Expand permutation is defined as –
EP(k1, k2, k3, k4) = (k4, k1, k2, k3, k2, k3, k4, k1)
After ep = 1 1 1 0 1 0 1 1
We perform XOR operation using the first key K1 with the output of expanded permutation.
Key-1 is - 1 0 1 0 0 1 0 0
(1 0 1 0 0 1 0 0) XOR (1 1 1 0 1 0 1 1) = 0 1 0 0 1 1 1 1
After XOR operation with 1st Key = 0 1 0 0 1 1 1 1
Again we divide the output of XOR into 2 halves of 4 bit each.
l = 0 1 0 0 and r = 1 1 1 1
We take the first and fourth bit as row and the second and third bit as a column for our S boxes.
S0 = [1,0,3,2
3,2,1,0
0,2,1,3
3,1,3,2]
S1= [0,1,2,3
2,0,1,3
3,0,1,0
2,1,0,3]
For l = 0 1 0 0
row = 00 = 0, column = 10 = 2
S0 = 3 = 11
For r = 1 1 1 1
row = 11 = 3, column = 11 = 3
S1 = 3 = 11
After first S-Boxes combining S0 and S1 = 1 1 1 1
S boxes gives a 2-bit output which we combine to get 4 bits and then perform permutation using the P4 table. P4 is defined as –
P4(k1, k2, k3, k4) = (k2, k4, k3, k1)
After P4 = 1 1 1 1
We XOR the output of the P4 table with the left half of the initial permutation table i.e. IP table.
(0 1 0 1) XOR (1 1 1 1) = 1 0 1 0
After XOR operation with left nibble of after ip = 1 0 1 0
We combine both halves i.e. right half of initial permutation and output of ip.
Combine 1 1 0 1 and 1 0 1 0
After combine = 1 0 1 0 1 1 0 1
Step-3:
Now, divide the output into two halves of 4 bit each. Combine them again, but now the left part should become right and the right part should become left.
After step 3 = 1 1 0 1 1 0 1 0
Step-4:
Again perform step 2, but this time while doing XOR operation after expanded permutation use key 2 instead of key 1.
* 4 1 2 3 2 3 4 1 pointed EP Sequence
Expand permutation is defined as - 4 1 2 3 2 3 4 1
After second ep = 0 1 0 1 0 1 0 1
After XOR operation with 2nd Key = 0 0 0 1 0 1 1 0
After second S-Boxes = 1 1 1 1
P4 is defined as - 2 4 3 1
After P4 = 1 1 1 1
After XOR operation with left nibble of after first part = 0 0 1 0
After second part = 0 0 1 0 1 0 1 0
l = 1 1 0 1 and r = 1 0 1 0
On the right half, we perform expanded permutation using EP table which converts 4 bits into 8 bits. Expand permutation is defined as –
EP(k1, k2, k3, k4) = (k4, k1, k2, k3, k2, k3, k4, k1)
After second ep = 0 1 0 1 0 1 0 1
We perform XOR operation using second key K2 with the output of expanded permutation.
Key-2 is - 0 1 0 0 0 0 1 1
(0 1 0 0 0 0 1 1) XOR (0 1 0 1 0 1 0 1) = 0 0 0 1 0 1 1 0
After XOR operation with 2nd Key = 0 0 0 1 0 1 1 0
Again we divide the output of XOR into 2 halves of 4 bit each.
l = 0 0 0 1 and r = 0 1 1 0
We take the first and fourth bit as row and the second and third bit as a column for our S boxes.
S0 = [1,0,3,2
3,2,1,0
0,2,1,3
3,1,3,2]
S1 = [0,1,2,3
2,0,1,3
3,0,1,0
2,1,0,3]
For l = 0 0 0 1
row = 01 = 1 , column = 00 = 0
S0 = 3 = 11
For r = 0 1 1 0
row = 00 = 0 , column = 11 = 3
S1 = 3 = 11
After first S-Boxes combining S0 and S1 = 1 1 1 1
S boxes gives a 2-bit output which we combine to get 4 bits and then perform permutation using the P4 table. P4 is defined as –
P4(k1, k2, k3, k4) = (k2, k4, k3, k1)
After P4 = 1 1 1 1
We XOR the output of the P4 table with the left half of the initial permutation table i.e. IP table.
(1 1 0 1) XOR (1 1 1 1) = 0 0 1 0
After XOR operation with left nibble of after first part = 0 0 1 0
We combine both halves i.e. right half of initial permutation and output of ip.
Combine 1 0 1 0 and 0 0 1 0
After combine = 0 0 1 0 1 0 1 0
After second part = 0 0 1 0 1 0 1 0
Step-5:
Perform inverse initial permutation. The output of this table is the cipher text of 8 bit.
Output of step 4 : 0 0 1 0 1 0 1 0
Inverse Initial permutation is defined as –
IP-1(k1, k2, k3, k4, k5, k6, k7, k8) = (k4, k1, k3, k5, k7, k2, k8, k6)
8-bit Cipher Text will be = 0 0 1 1 1 0 0 0
'Cryptography' 카테고리의 다른 글
| Meet-in-the-middle attack (0) | 2024.02.29 |
|---|---|
| Block Cipher modes of Operation (31) | 2024.02.29 |
| Block Cipher Design Principles (0) | 2024.02.29 |
| DES (Data Encryption Standard) (0) | 2024.02.28 |
| Simplified Data Encryption Standard Key Generation (63) | 2024.02.28 |