Lets start with the definition of CBC mode of operation. CBC stands for cipher block chaining.
Each block of plaintext is XORed with the previous ciphertext block before being encrypted. This way, each ciphertext block depends on all plaintext blocks processed up to that point. To make each message unique, an initialization vector must be used in the first block.
CBC is a way of randomizing the output of the encrypted value. It works by using an IV or initialization vector. The IV is a random value that is used against each block of your encrypted value. The first block of plain text is XORed with the IV and then that value is XORed with the next block and it keeps doing this until each block is XORed with the last one.

Hence we have to reverse XOR to find the bits that will result in our required Plain Text(PT). This practical involves a little calculation at the end. We will look into it and understand it in the simplest way possible.
For this practical we will need Mutillidae 2 that you can download from https://sourceforge.net/projects/mutillidae/ and Burp Suite.
I am dividing the practical in two parts:
- To get the required value in the PT from the altered bits in IV.
- To calculate and reverse XOR for the arbitrary values that we get in our PT and get the required value(000). This may not be clear now but will be clear by the end of part 1.
Let’s start with part 1:
Browse to your Mutillidae and open Owasp 2017->Broken Authentication and Session Management->Privilege Escalation->Via CBC-bit Flipping
We get to see the following page
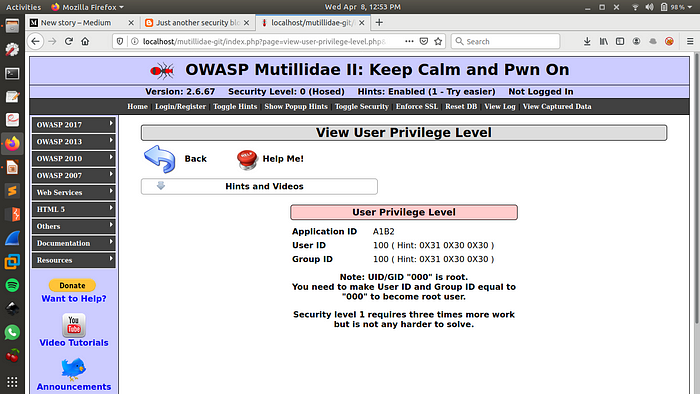
Our aim for this part will be to capture the request on burp suite and alter the bits in the IV and map the bits that brings the desired changes in PT. We have to change the values of User Id and Group Id to 000 for “Root Privilege Level”

In the above image we can see that the value of IV is available to us. We will now send this request to “Repeater” and start altering and mapping the changes

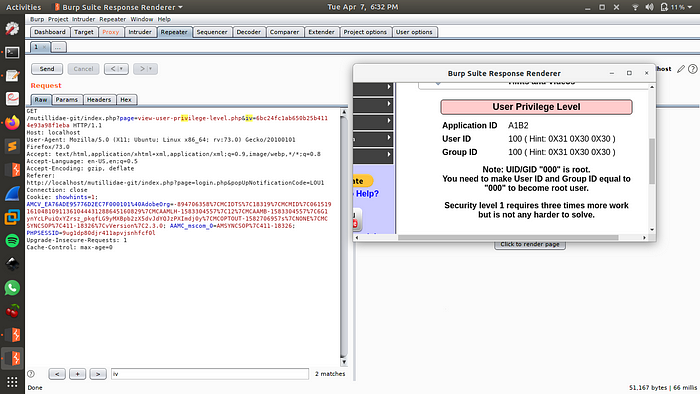
Now what we have to do is to change the bits in IV till we see the 0s in the User Id and Group Id. We will do this by replacing 2 bits at a time with ff and see the change in the Response Section by rendering the response as shown above.

We can see changes in the value of Application Id. We will keep changing the bits in similar manner till we reach User Id.

We have reached at the point were our given IV changes the User Id to e00. This value of IV is ffffffffff650b25b4114e93a98f1eba.
We will keep this value with us for part 2 and start proceeding in the similar way for changes in Group Id.
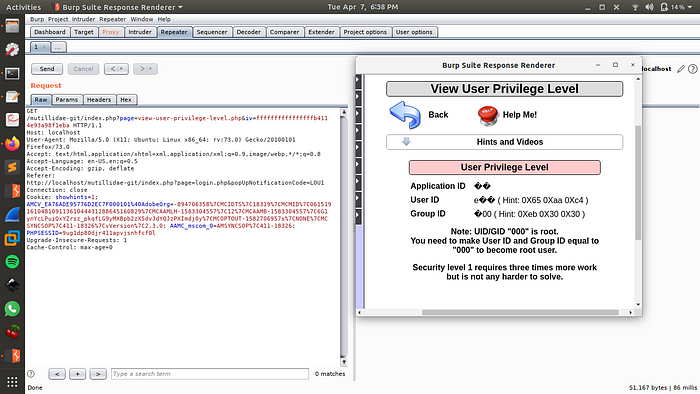
The value at which we get ?00 at Group Id is IV=ffffffffffffffffb4114e93a98f1eba. Now that we have values for both User and Group Ids we will proceed for the part 2 of the practical.
Lets move to part 2:
Now you may be wondering about the e and ? we are getting in our results while we actually needed 000. This is what I was talking about in the beginning of our practical. We have to change these values to 0.
Now we will deal with these values by some simple calculation.
First we have to take the final ff bits in our two results of User and Group Id IVs and replace them in the original IV value.
Original: 6bc24fc1ab650b25b4114e93a98f1eba
New: 6bc24fc1ff650bffb4114e93a98f1eba
Now we have to revise some concepts of CBC and then start calculating.
While encryption, we XORed IV to PT to get our CT. So here the IV that gave us the change was ff and the PT that was visible to us is e. So to find the actual CT we will simply XOR ff to hex value of e i.e 65 and we get 9a after calculation.
9a is the actual CT and now we need the required IV that will give us 0 in place of e. So we will again XOR 9a to hex of 0 i.e 30 and we get aa as the result.
Hence the logic can be memorized as:
First XOR for CT (IV xor PT)
Then XOR for IV (CT xor 30 i.e hex(0))
But what about that symbol in Group Id. I tried 22 in place of ff for Group Id and got 600 that can be changed to 000 as we did above.
Same steps:
First XOR for CT = 22 xor 36 i.e hex(6) = 14
Then XOR for IV = 14 xor 30 i.e hex(0) = 24
Hence we have aa and 24 as the required value of IV that will give us 000 or root in our practical. So let’s replace the values and send the request through repeater and see of it works.
Final IV = 6bc24fc1aa650b24b4114e93a98f1eba
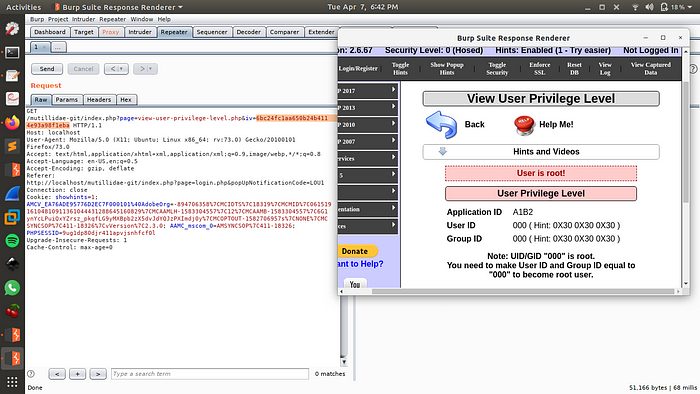
As you can see we have successfully changed the User and Group Id bits to 000 and have User as root.
Now copy the url from repeater and open it in the browser.

Thanks for reading.
'Cryptography' 카테고리의 다른 글
| The group Zp* (31) | 2024.03.11 |
|---|---|
| Padding oracles and the decline of CBC-mode cipher suites (117) | 2024.03.08 |
| AES Cipher (0) | 2024.03.07 |
| Advanced Encryption Standard (AES) (31) | 2024.03.07 |
| 일부 변화가 있었던 ARIA 찾아서 조지기 (0) | 2024.03.04 |