At CloudFlare, we’re committed to making sure the encrypted web is available to everyone, even those with older browsers. At the same time, we want to make sure that as many people as possible are using the most modern and secure encryption available to them. Improving the cryptography used by the majority requires a coordinated effort between the organizations building web browsers and API clients and those working on web services like CloudFlare. Cryptography is a two-way street. Even if we support the most secure cryptographic algorithms for our customers, web visitors won’t get the benefit unless their web client supports the same algorithms.
In this blog post we explore the history of one widely used cryptographic mode that continues to cause problems: cipher block chaining (CBC). We’ll explain why CBC has proven difficult to use safely, and how recent trends in the adoption of secure ciphers by web clients have helped reduce the web’s reliance on this technology. From CloudFlare’s own data, we’ve seen the percentage of web clients that support safer cipher modes (such as AEAD) rise from under 50% to over 70% in six months, a good sign for the Internet.
What’s in a block cipher?
Ciphers are usually grouped into two categories: stream ciphers and block ciphers. Stream ciphers encrypt data on a bit-by-bit basis. Plaintext and ciphertext are always the same length. Examples of pure stream ciphers are RC4 and ChaCha20. Although RC4 is no longer considered secure, we can still rely on ChaCha20 as a secure stream cipher for use on the web, but it was only recently standardized by the IETF and therefore does not have broad adoption.
Unlike stream ciphers, which can encrypt data of any size, block ciphers can only encrypt data in "blocks" of a fixed size. Examples of block ciphers are DES (8-byte blocks) and AES (16-byte blocks). To encrypt data that is less than one block long using a block cipher, you have several options. You can either turn the block cipher into a stream cipher (using something called counter mode, more on this later), or you can include extra bytes as padding to align the data to the block size. If the data is longer than one block, then the data needs to be split into multiple blocks that are encrypted separately. This splitting process is where things get tricky.
The naïve approach to encrypting data larger than the block size is called Electronic Code Book (ECB) mode. In ECB mode, you split your data into chunks that match the cipher’s block size and then encrypt each block with the same key. ECB turns out to be a very bad way to encrypt most kinds of data: if the data you are encrypting has redundant portions, say an image with many pixels of the same color, you end up with the "Tux" problem (demonstrated below). If two blocks have the same value, they will be encrypted to the same value. This property lets an attacker know which plaintext blocks match by looking at the ciphertext blocks.
For example, here’s what a high-resolution version of Linux’s "Tux" looks when encrypted in ECB mode:


Image from Filippo Valsorda’s blog
The fact that identical plaintext blocks are encrypted to identical ciphertext blocks gives an unwanted structure to encrypted data that reveals information about the plaintext.
One solution to this is to "chain" blocks together by taking the output of one encryption and mixing it into the input for the next block. There are several block cipher modes, but the one that was originally standardized in SSL (and continues to be used in TLS) is Cipher Block Chaining (CBC). In CBC, the plaintext of one block is combined with the ciphertext of the previous block using the exclusive OR operation (XOR). The first block is XOR’d with a randomly generated initialization vector (IV).


Decryption works by XORing the previous block of ciphertext (or the IV) into the output of the decryption.
CBC has some nice properties. The ciphertext produced by a block cipher is encrypted, so it (hopefully) looks random. In CBC, you’re mixing this random looking encrypted data into the plaintext, making it very unlikely that there will be patterns in the output. Another advantage is that decryption can be done in parallel to speed things up. However, CBC has proven to be more trouble than expected when used in the context of the HTTPS and the web.
How records are encrypted in TLS
TLS provides both encryption—via a cipher—and integrity—via a message authentication code (MAC). When SSL was originally designed, one open question was: should we authenticate the plaintext data, or should we encrypt and then authenticate the encrypted data? This is sometimes stated as MAC-then-encrypt or encrypt-then-MAC? They chose MAC-then-encrypt (encrypt the authenticated data) which has since proven to be the less than ideal choice.
In cryptographic protocol design, leaving some bytes unauthenticated can lead to unexpected weaknesses (this is known as the Cryptographic Doom Principle). When encrypting data using a block cipher mode like CBC, the last block needs to be padded with extra bytes to align the data to the block size. In TLS, this padding comes after the MAC. (There is a TLS extension, described in RFC 7366, that enables encrypt-then-MAC, but it’s rarely implemented.)
A TLS record has the following format. Each one has an 8-byte sequence number that is stored and incremented on each new one. The encrypted part of a request needs to add up to a multiple of 16 bytes, but for the purposes of this post, let’s assume that this length is 64 bytes (4 blocks).

In TLS, valid padding looks like a number preceded by that number of copies of itself. So, if the number is 0x00, it’s repeated 0 times:

If the number is 0x02, it’s repeated 0x02 times:

To decode a block, decrypt the entire message, look at the last byte, remove it, and remove that many bytes of padding. This gives you the location of the HMAC.
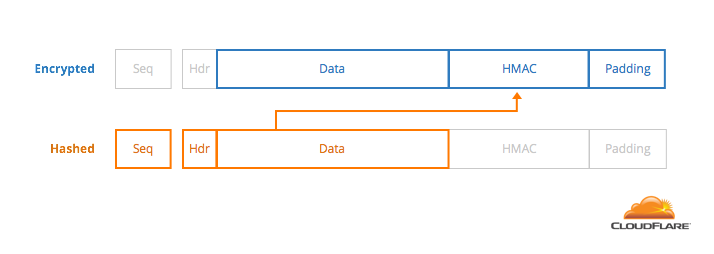
To compute the MAC, take the sequence number, the 5-byte header, and the message, then HMAC them using the shared integrity key.
Padding oracle
The problem with this construction is that it is susceptible to a technique called the padding oracle attack. This attack was first reported against TLS by Serge Vaudenay in 2002. A padding oracle is a way for an attacker with the ability to modify ciphertext sent to a server to extract the value of the plaintext.
Attackers don’t have to be an ISP or a government to get in the middle of requests. If they are on the same local network as their victim they can use a technique called ARP spoofing. By tricking the victim’s machine to forward data to the attacker’s machine instead of the router, they can read, modify and measure the time it takes for every encrypted message sent from the browser to the server. By injecting JavaScript into an unencrypted website the client is visiting, they can get the browser to repeatedly send requests to a target HTTPS site. The
'Cryptography' 카테고리의 다른 글
| HOTP and TOTP (31) | 2024.03.21 |
|---|---|
| The group Zp* (31) | 2024.03.11 |
| CBC-bit Flipping (56) | 2024.03.08 |
| AES Cipher (0) | 2024.03.07 |
| Advanced Encryption Standard (AES) (31) | 2024.03.07 |